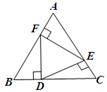
如图，在正三角形ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，FD⊥BC，则△DEF的面积与△ABC的面积之比等于（ ）
- A.1:3
- B.2:3
- C.
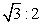
- D.
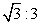
答案
正确答案：A
知识点：相似三角形的性质
在正三角形ABC中，∠A=∠B=∠C=60°，因为DE⊥AC，EF⊥AB，FD⊥BC，所以∠AFE=∠BDF=∠DEC=90°，所以∠DFE=∠DEF=∠FDE=60°，△DEF为等边三角形，所以△DEF∽△ABC，在直角三角形中，30°对的直角边是斜边的一半，设BD=m，则DF=
m，BF=2m，由△BDF≌△AFE，得AF=BD=m，则AB=3m，相似比为：3，面积比是1:3
略
WORD格式（
