已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异
于C,D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y.
(1)写出y与x之间的关系式 .( )

- A.
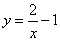
- B.
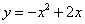
- C.
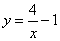
- D.
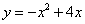
答案
正确答案:D
知识点:三等角模型
1.解题要点
∠EPM为斜直角,结合矩形的两个直角,可以利用三等角模型解决问题.
2.解题过程
如图,
在矩形ABCD中,∠C=∠D=90°,DC=AB=4,
∴∠PMC+∠MPC=90°.
∵∠EPM=90°,
∴∠DPE+∠CPM=90°,
∴∠DPE=∠CMP,
∴△DPE∽△CMP,
∴![]() .
.
∵点M是BC的中点,BC=2,
∴CM=BM=1.
∵PC=x,DE=y,
∴DP=4-x,
∴![]() ,
,
∴![]() .
.
故选D.
略







