(上接试题1)(2)当点P在边AD上移动时,能够证明△PDH的周长是一个定值,则这个定值为( )
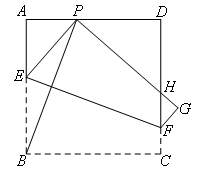
- A.12
- B.10
- C.8
- D.

答案
正确答案:C
知识点:角平分线的性质 翻折变换(折叠问题)
1.解题要点
①分析特征,辨识模型![]() 且为定值,由于已知的线段长只有正方形的边长,所以考虑将PH向正方形的边长上转化;
且为定值,由于已知的线段长只有正方形的边长,所以考虑将PH向正方形的边长上转化;
②围绕目标,转化条件
利用上一问的分析,∠APB=∠BPH,即BP是∠APH的角平分线,考虑角平分线的性质,过点B作PH的垂线,构造全等来转移边,如图所示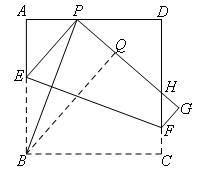
∴△BAP≌△BQP(AAS),
∴PA=PQ,BA=BQ=BC,
连接BH,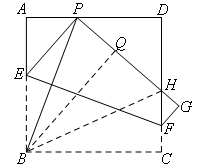
则△BQH≌△BCH(HL),
∴QH=CH,
∴PH=AP+HC,
∴PD+DH+PH=PD+DH+AP+HC=AD+DC=8.
∴△PDH的周长为8.
2.解题过程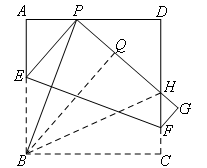
如图,过点B作BQ⊥PG于点Q,连接BH,
由题意,∠A=∠C=90°,AB=BC,
由上一问可知,∠APB=∠BPQ,
∴△BAP≌△BQP(AAS),
∴BA=BQ,PA=PQ,
∴BQ=BC,
∵∠BQH=∠BCH=90°,BH=BH,
∴△BQH≌△BCH(HL)
∴QH=CH,
∴PH=AP+HC,
∴PD+DH+PH=PD+DH+AP+HC=AD+DC=8.
∴△PDH的周长为8.
略








