（上接第1题）在图2中，D是线段BC上的任意一点，DE+DF与BG的关系仍然成立.下列3种思路中你认为可行的是(    )
思路①：连接AD，借助S_△ABD+S_△ACD=S_△ABC
思路②：过点D作DM⊥BG于点M，然后证明△BMD≌△DEB
思路③：连接EF，证明EF=BG

（1）①首先考虑类比第1题的思路、做法；
②对比第1题发现，D点作为中点变了，但垂直、线段间的关系没有变；
③从垂直、线段间的关系入手；
（2）①从垂直出发（BG，DE，DF都和垂直有关，可以考虑面积）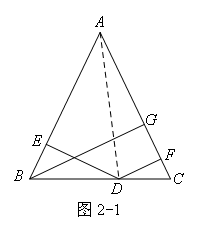

●如图2-1，连接AD
●根据S_△ABD+S_△ACD=S_△ABC，则
●可得DE+DF=BG
②从线段间的关系出发（考虑截长补短）

●如图2-2，过点D作DM⊥BG于点M，则四边形DMGF为矩形，DF=GM
●证明△BMD≌△DEB，可得BM=DE
●BG=BM+GM=DE+DF

略