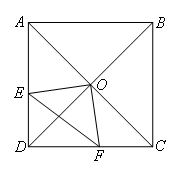
如图，在正方形ABCD中，对角线AC和BD相交于点O．点E，F分别在边AD，DC上．
若AE=4，CF=3，且OE⊥OF，则EF的长为(    )

思路：根据正方形的性质，可得OC=OD，OC⊥OD，
再结合OE⊥OF，想到旋转结构，则可证全等.
解题过程：
在正方形ABCD中，OC=OD，OC⊥OD．
∵OE⊥OF，
∴∠DOE=∠COF．
又∵∠ODE=∠OCF=45°，
∴△ODE≌△OCF（ASA），
∴CF=DE=3，
∴DF=CD-CF=AD-CF=4．
在Rt△DEF中，由勾股定理，得EF=5．
故选C．

略