在△ABC中，AB=AC，AB的垂直平分线DE与AC所在的直线相交于点E，垂足为点D，
连接BE．若AE=5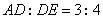，，则BE+CE的值为          ．

1．解题要点
①“与AC所在的直线相交于点E”，提示我们需进行分类讨论．
②经常考查分类讨论的点有以下几种．
无图：常含有关键词，如高（形内高、形外高），直线，射线．
指代不明：如两个三角形的面积之比为9:10，等腰三角形一腰上的高与另一边的
夹角为25°，圆与圆相切（内切、外切）．
位置不确定：如运动过程中直线与圆相切，弦在圆心同侧、异侧，动点问题．
对应关系不确定：如全等，相似．
存在性问题：如等腰三角形、平行四边形存在性．
2．解题过程
①当点E在线段AC上时，如图所示，

在△ADE中，∵AE=5，
∴AD=3，DE=4，
∴AB=AC=2AD=6，
∴CE=1．
∵BE=AE=5，
∴BE+CE=6．
②当点E在线段CA的延长线上时，如图所示，

在△ADE中，∵AE=5，
∴AD=3，DE=4，
∴AB=AC=2AD=6，
∴CE=11．
∵BE=AE=5，
∴BE+CE=16．
综上，BE+CE的值为6或16．

略