如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为( )

- A.2
- B.
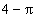
- C.
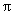
- D.
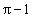
答案
正确答案:B
知识点:直角三角形斜边中线等于斜边一半 圆面积
共分为2大部分:①找出点M运动的路径;②求出路径围成的图形面积
①思路:
a.起始位置、特殊位置:点Q,R分别在点A,B处,此时点M在AB的中点;同理可得,点M经过BC,CD,DA的中点;
b.运动路径:当点Q在AB上运动,R在BC上运动时,QR为定长2,且M始终为QR的中点,结合∠B=90°,可知BM=![]() =1,说明M的路径为以B为圆心,1为半径的
=1,说明M的路径为以B为圆心,1为半径的![]() ,同理可得点M的运动路径为4段
,同理可得点M的运动路径为4段![]() ,如图所示:
,如图所示: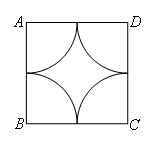
故所求面积为: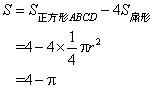
故选B
略








