已知: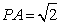 ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.如图,当∠APB=45°时,PD的长为( )
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.如图,当∠APB=45°时,PD的长为( )
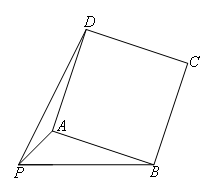
- A.
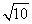
- B.

- C.
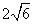
- D.
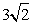
答案
正确答案:B

分析:看到∠APB=45°,考虑过点A向PB作垂线,得到等腰直角△APE,求出![]() ,又由于AB=AD,即等线段共顶点,故考虑旋转解题,把△APD绕点A顺时针旋转90°得到△AFB,可证△APF为等腰直角三角形,进而得到∠BPF为直角三角形,且BP及PF的长均易求得,根据勾股定理可计算出FB的长,即可得到PD的长.
,又由于AB=AD,即等线段共顶点,故考虑旋转解题,把△APD绕点A顺时针旋转90°得到△AFB,可证△APF为等腰直角三角形,进而得到∠BPF为直角三角形,且BP及PF的长均易求得,根据勾股定理可计算出FB的长,即可得到PD的长.
过A点作AE⊥PB于点E,如图,
∵∠APB=45°,
∴△APE为等腰直角三角形.
又∴![]() ,
,
∴![]() .
.
∵PB=4,
∴BE=PB-PE=3.
在Rt△AEB中,![]() ,
,
∵AD=AB,∠DAB=90°,
∴把△APD绕点A顺时针旋转90°得到△AFB,AD与AB重合,PA旋转到AF的位置.如图,
∴AP=AF,∠PAF=90°,PD=FB,
∴△APF为等腰直角三角形.
∴∠APF=45°.
∴∠BPF=∠APB+∠APF=90°.
在Rt△FBP中,PB=4,PF=2,
∴![]()
∴![]()
故选B.
略








