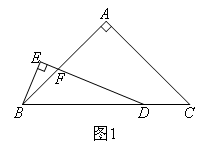
在△ABC中,∠A=90°,点D在BC边上, ,BE⊥DE,垂足为点E,
,BE⊥DE,垂足为点E,
DE与AB相交于点F.
(1)如图1,当AB=AC时,BE和DF之间的数量关系为( )
- A.DF=2BE
- B.BE=2DF
- C.
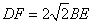
- D.
答案
正确答案:A
知识点:中考数学几何中的类比探究
点击查看解析视频:http://v.xxt.cn/course/video.do?id=13051
1.解题要点
①要研究两条线段之间的数量关系,考虑放到两个三角形中,利用相似求比例,
BE在Rt△BEF中,需要将DF放到某一个直角三角形中.
②考虑![]() ,过点D作AC的平行线交AB于点G,会出现角平分线,且由于∠A是直角,能够把DF放到Rt△DGF中,此时△BEF∽△DGF,但是BE和DF不是对应边,不能用相似比来求.
,过点D作AC的平行线交AB于点G,会出现角平分线,且由于∠A是直角,能够把DF放到Rt△DGF中,此时△BEF∽△DGF,但是BE和DF不是对应边,不能用相似比来求.
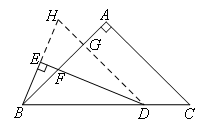
③有角平分线+垂直,延长BE,交DG的延长线于点H,出现三线合一,BH=2BE,
且△BGH≌△DGF,则![]() ,可以得到DF=2BE.
,可以得到DF=2BE.
④整个证明的路线图是:过点D作AC的平行线交AB于点G,交BE的延长线于点H;三线合一得到BH=2BE;△BGH≌△DGF;利用相似比得到结果.
2.解题过程
如图,过点D作AC的平行线交AB于点G,交BE的延长线于点H.
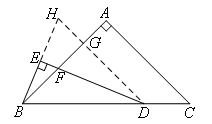
则∠BDH=∠C,∠BGD=∠A=90°,
∴△BGD∽△BAC,
∴![]() .
.
∵![]() ,BE⊥DE,
,BE⊥DE,
∴BH=2BE.
∵∠GDF+∠GFD=∠EBF+∠EFB=90°,∠GFD=∠EFB,
∴∠GDF=∠EBF.
∵∠BGH=∠DGF=90°,
∴△BGH≌△DGF,
∴![]() ,即
,即![]() ,
,
∴DF=2BE.
略








