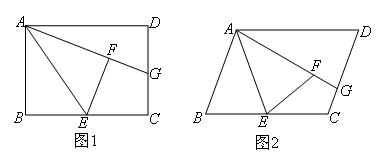
如图1，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G．容易得到GF=GC．如图2，将图1中的矩形ABCD改为平行四边形ABCD，其他条件不变，为了证明GF=GC，下列选项中添加的辅助线最合适的是(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=13049
1．解题要点
①首先需要弄清楚图1中的结论是如何证明的．
要证明两条线段相等，可以考虑放到两个三角形中证明全等，所以连接EG，
此时GF和GC分别在Rt△GFE和Rt△GCE中，由折叠和中点可以得到EF=EC，
由HL可以得到Rt△GFE≌Rt△GCE．

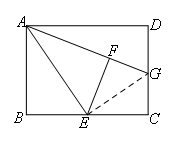
证明的路线图是：连接EG；EF=EC；Rt△GFE≌Rt△GCE（HL）；GF=GC．
②利用上述路线图尝试解决图2的问题，发现△GFE和△GCE不是直角三角形，
证明全等缺乏条件，思路进行不下去，需要换思路．
③要证明两条线段相等，还可以放到同一个三角形中证明等腰，
所以在图1中连接FC，证明∠GFC=∠GCF．

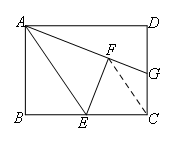
∵EF=EC，
∴∠EFC=∠ECF．
∵∠GFE=∠GCE，
∴∠GFC=∠GCF．
证明的路线图是：连接FC；∠EFC=∠ECF，∠GFE=∠GCE；∠GFC=∠GCF；结论成立．
④照搬上述路线图，解决图2中的问题，发现思路能够进行下去．
2．解题过程
如图，连接FC．

由折叠可得，BE=EF，∠B=∠AFE．
∵E是BC的中点，
∴EC=BE=EF，
∴∠EFC=∠ECF．
在平行四边形ABCD中，∠B+∠GCE=180°．
又∵∠AFE+∠GFE=180°，
∴∠GFE=∠GCE，
∴∠GFC=∠GCF，
∴GF=GC．

略