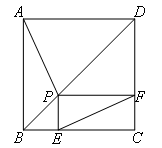
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,
连接EF,AP,则下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;
⑤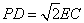 .其中正确的是( )
.其中正确的是( )
- A.①②③④
- B.①②④⑤
- C.②③④⑤
- D.①③④⑤
答案
正确答案:B
知识点:正方形的性质 全等三角形的判定与性质
如图,延长FP交AB于点N,延长AP交EF于点M,连接PC.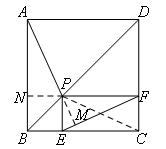
由题意可知,四边形BNPE,四边形PECF均为矩形,
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
又∵BP=BP,
∴△ABP≌△CBP(SAS),
∴AP=CP.
在矩形PECF中,CP=EF,
∴AP=EF,①正确.
由△ABP≌△CBP可得,∠PAN=∠PCE,
又∵∠PFE=∠PCE,
∴∠PFE=∠PAN,
∴∠PFE+∠FPM=∠PAN+∠APN=90°,
∴∠PMF=90°,
∴AP⊥EF,②④正确.
P是BD上任一点,因而△APD是等腰三角形不一定成立,故③错误.
由题意可知,△PDF为等腰直角三角形,
∴![]() ,⑤正确.
,⑤正确.
综上,正确的是①②④⑤,
故选B.
略








