如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为( )

- A.3
- B.5
- C.
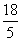
- D.

答案
正确答案:C
知识点:勾股定理之折叠问题
1.解题要点
对于此类求解面积的问题,关键是找到对应图形的底和高.
此题中阴影部分可以DE为底,过点G作底边DE上的高,求出底和高即可.
设出底DE,表达AE,在Rt△AGE中使用勾股定理求AE,
进而求DE,借助等积公式求高,则可求解面积.
2.解题过程
如图,过点G作GH⊥AD于点H.
由折叠得,∠AGE=∠CDE=90°,AG=CD=AB=4,GE=DE.
设DE=x,则GE=x,AE=8-x.
在Rt△AGE中,由勾股定理得,
AG2+GE2=AE2,即42+x2=(8-x)2,
解得,x=3.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故选C.
略








