如图,BD,BE分别是Rt△ABC的斜边AC上的中线与高线.若AB=4,BC=3,
则AD:DE:EC=( )
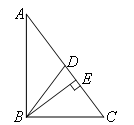
- A.5:3:4
- B.25:9:16
- C.25:7:18
- D.3:2:1
答案
正确答案:C
知识点:勾股定理 直角三角形斜边中线等于斜边一半 等积公式
1.思路分析
①梳理信息,明确目标.
本题要求三条线段的长度之比,明显需要计算出各线段长.
②合理转化与计算.
BD是斜边中线,直接计算斜边长的一半,即可得BD的长;
BE为斜边上的高,根据等积公式可得BE的长,
再根据勾股定理可得DE的长,CD-DE即为EC.
2.解题过程
在Rt△ABC中,AB=4,BC=3,
∴![]() .……梳理信息
.……梳理信息
∵BD是斜边AC上的中线,
∴BD=AD=CD=![]() .……合理转化,计算
.……合理转化,计算
∵BE是AC上的高,
∴![]() .……合理转化,计算
.……合理转化,计算
在Rt△BDE中,BD=![]() ,BE=
,BE=![]() ,
,
由勾股定理得,![]() ,
,
∴EC=![]() ,
,
∴AD:DE:EC=25:7:18.
故选C.
略








