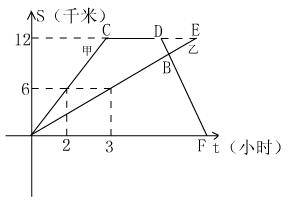
甲乙两名同学进行登山比赛,图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中,各自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:(1)分别求出甲、乙两同学登山过程中路程s(千米)与时间t(时)的函数解析式;(不要求写出自变量的取值范围)(2)当甲到达山顶时,乙行进到山路上的某点A处,求A点距山顶的距离;(3)在(2)的条件下,设乙同学从A点继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙同学相遇,此时点B与山顶距离为1.5千米,相遇后甲、乙各自沿原路下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
答案
(1)![]() ,
,![]() ;
;
(2)4千米;
(3)6千米.
知识点:一次函数的应用
(1)![]() ,
,![]() ;
;
(2)甲到山顶时,用时12÷3=4(小时),乙此时走了4×2=8(千米),那么A距山顶12-8=4(千米);
(3)甲从山顶开始返回时,乙走了2×(4+1)=10(千米)。乙还有2千米达到山顶。如果把此刻当做另一个起点,相遇时,甲走了1.5千米,则乙走了0.5千米,即甲在同样时间内走的路程是乙的三倍,乙的速度是2(千米/小时),∴甲的速度是6(千米/小时)。从甲下山开始,乙到山顶又用了1小时,此时甲行走6×1=6(千米),此时甲距山脚还有12-6=6(千米).
略








