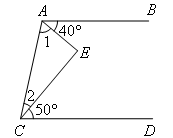
如图，AB∥CD，∠BAE=40°，∠DCE=50°，求∠E的度数．

解：                
即∠BAE+∠1+∠2+∠DCE=180°
∵∠BAE=40°，∠DCE=50°（已知）
∴∠1+∠2=180°-∠BAE-∠DCE
         =180°-40°-50°
         =90°（等式性质）
∵∠1+∠2+∠E=180°（三角形的内角和等于180°）
∴∠E=180°-（∠1+∠2）
     =180°-90°
     =90°（等式性质）
横线处应填写的过程恰当的是(    )

• A.
  
• B.
  
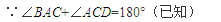
• C.
  
• D.
  

答案

正确答案：A

知识点：平行线的性质  三角形内角和定理  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>