已知:如图,AB=EF,BC=FG,AC=EG,D为BC中点,H为FG中点,求证:AD=EH.
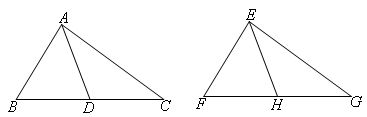
证明:如图,
在△ABC与△EFG中

∴
∴
∵D为BC中点,H为FG中点

∵BC=FG
∴BD=FH
在△ABD与△EFH中
∴△ABD≌△EFH( )
∴AD=EH.
① ;②
;②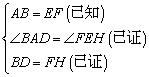 ;③
;③ ;
;
④∠BAD=∠FEH(全等三角形对应角相等);⑤∠B=∠F(全等三角形对应角相等);
⑥SSS;⑦SAS;⑧△ABC≌△FEG(SSS);⑨△ABC≌△EFG(SSS).
以上空缺处依次所填正确的是( )
- A.⑨⑤①⑦
- B.⑨④②⑦
- C.⑧⑤③⑥
- D.⑧④①⑦
答案
正确答案:A

略









 ;②
;②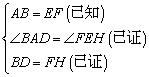 ;③
;③ ;
;