(上接第3题)(2)当△BOM的面积最大时,连接AM,若P为坐标平面内一点,
且△BOP∽△OAM,则点P的坐标为( )
- A.
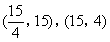
- B.
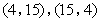
- C.
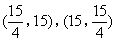
- D.
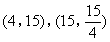
答案
正确答案:C
知识点:相似三角形的存在性
1.解题要点
①观察题目特征,属于相似三角形的存在性问题,目标三角形确定,
可以求出△OAM的各边长.
②△BOP中,只有点P是动点,
若△BOP∽△OAM,可以设出点P的坐标,表达出△BOP的各边长,
利用三边对应成比例的两个三角形相似,来求出两个三角形相似时点P的坐标.
显然这种方法思维链条比较短,但是计算量比较大.
③对于②中所说的方法,同学们可自行尝试.
这里采用相似三角形的另一个判定定理,
即两边对应成比例且夹角对应相等的两个三角形相似,
虽然∠AOM度数很难求出,但是可以控制旁边的两个小角相等.
④抛物线属于干扰图形,可以去掉.
2.解题过程
各点的位置如图所示,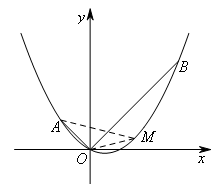
∵![]() ,
,
∴![]() .
.
①如图,当点P在OB上方时,过点B作y轴的平行线FG,交x轴与点F,
则∠AOE=∠OBF=45°,∠AOM=∠OBP,
∴∠MOF=∠PBG.
如图,过点M作MN⊥OF于点N,过点P作PQ⊥BG于点Q,
则△MON∽△PBQ,且![]() ,
,
∴![]() .
.
由![]() 得,
得,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
②如图,当点P在OB下方时,类比①可作辅助线,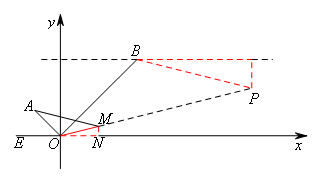
照搬①中的思路求解,可得![]() .
.
通过作图以及结果我们可以看到,两个点P其实是关于直线OB对称的.
综上,符合题意的点P的坐标为![]() .
.
略







