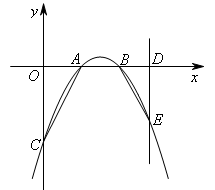
如图,已知二次函数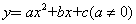 的图象经过A(1,0),B(2,0),
的图象经过A(1,0),B(2,0),
C(0,-2)三点,直线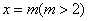 与x轴交于点D,与抛物线交于点E.连接AC,BE,若△BDE和△AOC相似,则点E的坐标为( )
与x轴交于点D,与抛物线交于点E.连接AC,BE,若△BDE和△AOC相似,则点E的坐标为( )
- A.
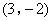
- B.
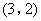
- C.
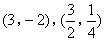
- D.
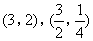
答案
正确答案:A
知识点:相似三角形的存在性
1.解题要点
①首先根据三点坐标,求出函数解析式.
②对目标图形进行研究,目标△AOC是固定的直角三角形,两直角边之比为1:2;
△BDE中,B是定点,D,E是动点,∠BDE=90°属于不变特征,
若两个三角形相似,只需满足![]() .
.
③根据D,E两点的坐标表达线段长,利用②中的比例关系建等式.
2.解题过程
设抛物线的解析式为![]() ,
,
∵C(0,-2)在抛物线上,
∴![]() ,
,
∴![]() .
.
由题意可得,![]() ,
,![]() ,
,
△AOC中,OA=1,OC=2,
△BDE中,BD=m-2,![]() .
.
①当![]() 时,△BDE∽△AOC,
时,△BDE∽△AOC,![]() ,解得
,解得![]() ,
,
∴![]() .
.
②![]() 时,△EDB∽△AOC,
时,△EDB∽△AOC,![]() ,解得
,解得![]() ,不符合题意.
,不符合题意.
综上,符合题意的点E的坐标为![]() .
.
略








