如图，在四边形ABCD中，AD=DC，∠ADC=∠ABC=90°，DE⊥AB于点E．若四边形ABCD面积为16，则DE的长为(    )

分析：
由AD=DC，AD⊥DC，可考虑将AD绕点D逆时针旋转90°到CD，
如此，可将△ADE同步进行旋转．
解题过程：
如图，过点D作DE的垂线交BC的延长线于点F．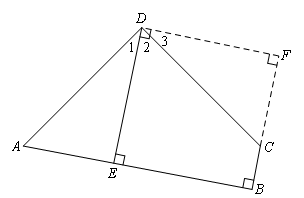

∵AD⊥DC，FD⊥DE，
∴∠1+∠2=90°，∠3+∠2=90°，
∴∠1=∠3．
∵DE⊥AB，FD⊥DE，CB⊥BE，
∴四边形DEBF是矩形，
∴∠F=90°，
∴∠DEA=∠DFC=90°．
∵AD=CD，
∴△ADE≌△CDF（AAS），
∴DE=DF，
∴四边形DEBF是正方形．
∵四边形ABCD的面积为16，
∴正方形DEBF的面积为16，
∴DE=4．
故选C．

略