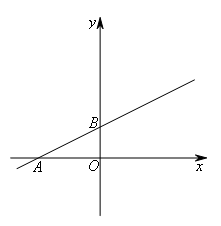
如图,直线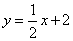 与x轴、y轴分别交于A,B两点,C是直线
与x轴、y轴分别交于A,B两点,C是直线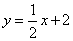 上不与A,B重合的动点.过点C的另一直线CD与y轴相交于点D,若△BCD与△AOB全等,则点C的坐标为( )
上不与A,B重合的动点.过点C的另一直线CD与y轴相交于点D,若△BCD与△AOB全等,则点C的坐标为( )
- A.
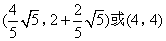
- B.
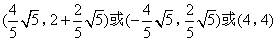
- C.
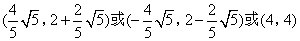
- D.
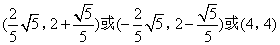
答案
正确答案:C
知识点:一次函数之存在性问题 全等三角形的存在性
1.解题要点
①首先研究基本图形,得到OB=2,OA=4;
②分析△BCD与△AOB,目标△AOB是直角三角形,且两直角边分别为2和4,若两个三角形全等,需要保证△BCD是直角三角形,且两直角分别为2和4;
③首先三个顶点轮流当直角顶点,再控制两直角边为2和4,进行分类讨论,过程中可结合题意排除不可能的情形.
2.解题过程
由直线![]() 知,OB=2,OA=4,
知,OB=2,OA=4,
∴△AOB是两直角边分别为2和4的直角三角形.
①画图分析,易知![]() .
.
②当∠BDC=90°时,画出符合题意的图形,
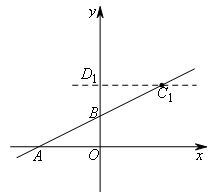
此时![]() ,
,
∴![]() .
.
③当∠BCD=90°时,画出符合题意的图形,过点![]() 作
作![]() 轴于点E.
轴于点E.
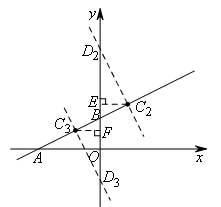
此时![]() ,
,
∴![]() .
.
同理,过点![]() 作
作![]() 轴于点F,
轴于点F,
则![]() ,
,
∴![]() .
.
综上,符合题意的点C的坐标为![]() .
.
略








