在平面直角坐标系中,已知点A(1,k)和点B(-1,-k)为二次函数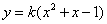 的图象上的两点,二次函数图象的顶点为Q,若△ABQ是以AB为斜边的直角三角形,则k的值为( )
的图象上的两点,二次函数图象的顶点为Q,若△ABQ是以AB为斜边的直角三角形,则k的值为( )
- A.
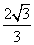
- B.
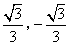
- C.
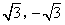
- D.
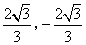
答案
正确答案:D
知识点:直角三角形的存在性
1.解题要点
①根据题意需要对k进行分类,首先分析![]() 时的情况,
时的情况,
然后照搬,分析![]() 时的情况;
时的情况;
②分析目标△ABQ,易得![]() ,由于AB是斜边,所以点Q为直角顶点;
,由于AB是斜边,所以点Q为直角顶点;
③在坐标系背景下知道了三个顶点坐标,若分析点Q为直角顶点,可以利用勾股定理逆定理,三等角模型,![]() ,这里采用三等角模型来解决问题,其他方法同学们可自行尝试;
,这里采用三等角模型来解决问题,其他方法同学们可自行尝试;
④结合题干,A(1,k)和B(-1,-k)关于原点对称,若△ABQ是以AB为斜边的直角三角形,也可以利用OA=OB=OQ来解决问题.
2.解题过程
由题意得![]() .
.
方法一:
①当![]() 时,画出符合题意的草图,如图所示,
时,画出符合题意的草图,如图所示,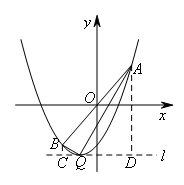
过点Q作直线![]() ∥x轴,过点B作BC⊥
∥x轴,过点B作BC⊥![]() 于点C,过点A作AD⊥
于点C,过点A作AD⊥![]() 于点D,
于点D,
易知△BCQ∽△QDA,
∴![]() .
.
∵![]() ,
,
∴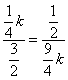 ,解得
,解得![]() .
.
∵![]() ,
,
∴![]() .
.
②当![]() 时,利用上述方法,同理可求,
时,利用上述方法,同理可求,![]() .
.
综上,符合题意的k的值为![]() .
.
方法二:以![]() 的情况为例,
的情况为例,
∵点A和点B关于原点对称,
∴A,O,B三点共线.
当∠BQA为直角时,OQ=OB=OA,表达出OQ和OA的长,
利用![]() ,即
,即![]() ,也可求得k的值.
,也可求得k的值.
略







