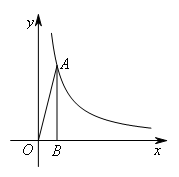
如图,点A在反比例函数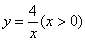 的图象上,且
的图象上,且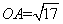 ,AB⊥x轴于点B,
,AB⊥x轴于点B,
AB=4OB.若P是y轴上一动点,则当△OAP是直角三角形时,点P的坐标为( )
- A.
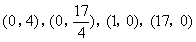
- B.

- C.

- D.
答案
正确答案:C
知识点:直角三角形的存在性
1.解题要点
①首先研究基本图形,根据信息能够求出点A的坐标为(1,4);
②分析目标△OAP,O,A是定点,P是y轴上一动点,若△OAP是直角三角形,需要根据直角顶点进行分类,把三个顶点轮流作直角顶点进行分析;
③对于直角,需要结合题目背景灵活处理,如以点A为直角顶点时,可以借助坐标系背景用函数解析式来求点坐标,也可以借助相似来解决问题.
2.解题过程
由题意得,![]() ,
,
当∠AOP=90°时,显然不成立.
当∠OAP=90°时,过点A作AP⊥OA,交y轴于点P,如图所示,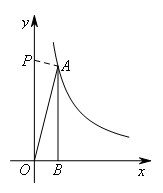
易知△AOB∽△OPA,
∴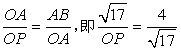 ,
,
∴![]() ,
,
∴![]() .
.
当∠APO=90°时,过点A作AP⊥y轴于点P,如图所示,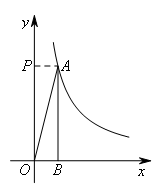
易得四边形APOB为矩形,
∴![]() .
.
综上所述,符合题意的点P的坐标为![]() .
.
略








