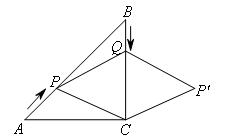
如图，在Rt△ABC中，∠ACB=90°，AC=BC=9cm．点P从点A出发，沿AB方向以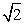
cm/s的速度向终点B运动；同时点Q从点B出发，沿BC方向以1cm/s的速度向终点C运动．将△PQC沿BC翻折，点P的对应点为点
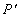．设点Q运动的时间为t秒，当四边形
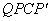为菱形时，t的值为( )
．设点Q运动的时间为t秒，当四边形
- A.
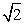
- B.
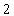
- C.
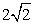
- D.
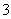
答案
正确答案：D
知识点：动点问题 菱形的存在性（转等腰）
由题意得，t的取值范围是
．
∵四边形
是由△PQC翻折得到的，
∴
．
若四边形为菱形，只需要满足PQ=PC即可．
如图，过点P作AC，BC的垂线，垂足分别为D，E．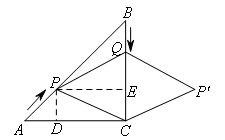
则△APD是等腰直角三角形，四边形PDCE是矩形，
∴
．
∵PQ=PC，PE⊥BC，
∴QE=EC=t．
∵BQ=t，
∴BC=3t．
又∵BC=9，
∴t=3（符合题意）．
综上得，四边形为菱形时，t的值为3．
略
WORD格式（
