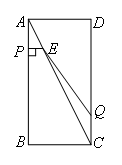
如图,在矩形ABCD中,AB=8,BC=4.点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度.过点P作PE⊥AB交AC于点E,连接EQ.在点P,Q运动的过程中,设运动时间为t秒,则当△CEQ是等腰三角形时,t的值为( )
- A.
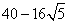 ,
,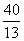
- B.
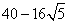 ,
,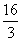
- C.
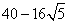 ,
,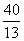 ,
,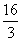
- D.
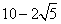 ,
,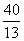 ,
,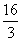
答案
正确答案:C
1.解题要点
①首先研究基本图形,AB=DC=8,BC=AD=4,![]() ,
,
△ABC和△ADC都是三边关系为![]() 的直角三角形.
的直角三角形.
②分析动点的运动状态,点P和点Q的运动状态如图所示,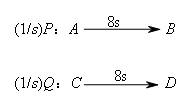
∴![]() .
.
表达动点走过的路程,AP=CQ=t,
∴![]() .
.
②分析目标△CEQ,C是定点,点E和点Q是动点,但∠ECQ固定,
符合“夹角固定、两点动”的特征,
可以借助三线合一找相似来解决问题,分类画图,根据特征求解.
2.解题过程
①当CE=CQ时,如图所示,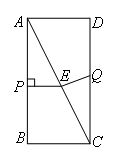
则![]() ,解得
,解得![]() ,符合题意.
,符合题意.
②当CQ=EQ时,如图所示,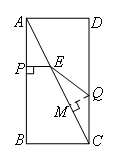
过点Q作QM⊥AC于点M,
则CM=EM,△CMQ∽△CDA,
∴![]() ,
,
即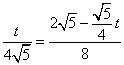 ,解得
,解得![]() ,符合题意.
,符合题意.
③当CE=EQ时,如图所示,
延长PE交CD于点N,则EN⊥CD,
∴CN=NQ.
∵△CNE∽△CDA,
∴![]() ,即
,即 ,
,
解得![]() ,符合题意.
,符合题意.
综上,符合题意的t的值为![]() ,
,![]() ,
,![]() .
.
略








