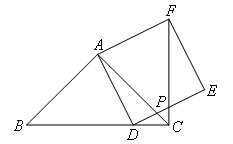
如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点,连接AD,以AD为一边在AD的右侧作正方形ADEF,CF交DE于点P.若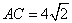 ,CD=2,则线段CP的长为( )
,CD=2,则线段CP的长为( )
- A.1
- B.2
- C.
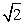
- D.
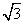
答案
正确答案:A
知识点:三角形中位线 全等三角形的性质与判定 等腰直角三角形的性质和判定
如图,过点A作AM⊥BC于点M,
过点E作EN⊥BC,交BC的延长线于点N.
由题意可得,∠ACB=45°,△AMC为等腰直角三角形,∠DAF=90°,AD=AF.
∵![]() ,
,
∴![]() .
.
∵CD=2,
∴MD=2.
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF.
又∵AB=AC,AD=AF,
∴△BAD≌△CAF,
∴∠B=∠ACF=45°,
∴∠FCD=∠ACB+∠ACF=90°,即FC⊥BC,FC∥EN.
易证△AMD≌△DNE,
∴AM=DN=4,DM=EN=2,
∴CN=4-2=2,
∴C为DN的中点,CP为△DNE的中位线,
∴![]() .
.
略








