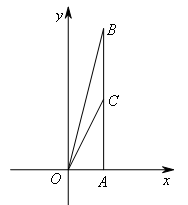
如图，在Rt△AOB中，∠A=90°，OA=2，AB=8，C为AB边的中点，以O为坐标原点建立平面直角坐标系，使点A在x轴正半轴上．以原点O为顶点的抛物线经过点C，将该抛物线沿线段OC移动，使其顶点M始终在线段OC上（包括端点O，C），设抛物线与y轴的交点为D，与AB边的交点为E．
（1）当四边形BDOC为平行四边形时，抛物线的解析式为(    )

• A.
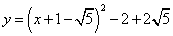
• B.
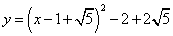
• C.
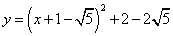
• D.

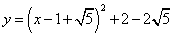
答案

正确答案：A

知识点：二次函数平移  平行四边形的存在性  

由题意得，C（2，4），
∴直线OC：y=2x．
设原抛物线的解析式为，
将点C（2，4）代入可得，
∴原抛物线的解析式为．
设，
则移动后抛物线的解析式为，如图所示，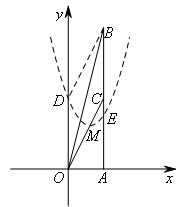

∴．
在四边形BDOC中，只有点D是动点，且OD∥BC始终不变，
若四边形BDOC是平行四边形，
只需OD=BC，
∴，
解得，．
∵，
∴，
∴所求抛物线的解析式为．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>