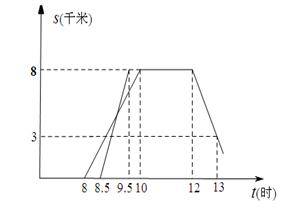
某班师生组织植树活动，上午8时从学校出发，到植树地点植树后原路返校，如图为师生离校路程s与时间t之间的图象.

请回答下列问题：(1)求师生何时回到学校？(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点.请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程；(3)如果师生骑自行车上午8时出发,到植树地点后，植树需2小时，要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.

（1）从图上可以看出，学校离植树地点8km，最后一段为师生从植树地点回学校时离校路程s与时间t之间的函数关系，已知两点（12，8）和（13,3），可以求出师生从植树地点回学校时离校路程s与时间t之间的函数关系为y=-5x+68，当回到学校时，y=0，则x=13.6，即13时36分回到学校.（2）由题意，三轮车运送树苗的函数图象经过两点（8.5，0）和（9.5，8），可以画出该三轮车运送树苗时,离校路程s与时间t之间的图象.师生步行从学校到植树地点，2小时走了8km，速度为4km/h，骑三轮车从学校到植树地点1小时走了8km，速度为8km/h.设t 时刻相遇，则，得到t=9，所以三轮车追上师生时,离学校的路程km.（3）上午8时出发，要求14时前返回，则去的时间加上植树的时间加上返回的时间要小于等于6小时.设植树点与学校的路程为s，则，解得，所以13km、15km、17km都符合要求.

用一次函数解决图象类问题，不能抓住两个关键点：特殊点的坐标所代表的含义；寻找两点确定一次函数表达式。