如图，抛物线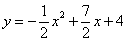与x轴正半轴交于点A，与y轴交于点B，点C在y轴上，且AB=AC．若一条与y轴重合的直线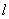以每秒2个单位长度的速度向右平移，分别交x轴、线段AB和抛物线于点E，M，P，连接PA，PB．设直线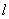移动的时间为t秒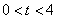（），当四边形PBCA的面积最大时，t的值及四边形PBCA的最大面积分别为(    )

• A.4，64
• B.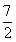，72
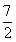• C.，64
• D.2，64

答案

正确答案：D

知识点：二次函数背景下的面积问题  铅垂法求面积  

∵，
∴A，B．
∵AB=AC，
∴C．
四边形PBCA中，A，B，C为定点，P为动点，考虑将四边形PBCA分成△ABC和△ABP来计算．
，
，
，
∴，
易知直线AB：，
由题意得，即点M和点P的横坐标均为，
∴，，
∴，
∴．
∵，
∴当时，有最大值，最大值为64．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>