如图，抛物线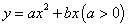经过A（1，4），B（-2，-2）两点，过点A作
直线AC∥x轴，交抛物线于点C．若抛物线上存在一点D（不与点C重合），使得△ABD与△ABC的面积相等，则点D的坐标为(    )

容易求得抛物线的解析式为，点C（-4，4），直线AB：，
△ABD和△ABC有公共边AB，所以利用平行来转化面积进行计算．
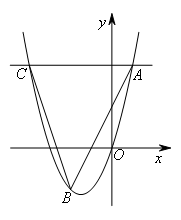
①过点C作CM∥AB交抛物线于另一点M，如图所示，

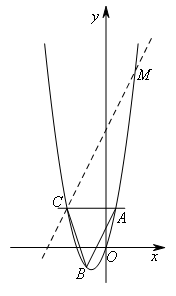
则直线CM：，
联立，解得，
∴点M（3，18）．
②直线CM是由直线BA向上平移10个单位得到的，
将直线BA向下平移10个单位，得到直线：，如图所示，

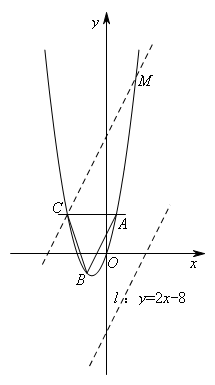
联立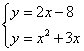，方程无解，
∴直线：与抛物线没有交点，此种情况点M不存在．
综上所述，点M（3，18）．

略