实数x、y、z满足x+y+z=5,xy+yz+zx=3,则z的最大值是( )
- A.
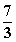
- B.
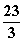
- C.
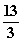
- D.
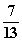
答案
正确答案:C
知识点:一元二次方程
对于三元代数式中某一字母的最值问题,通常利用一元二次方程的根与系数关系,构造一个一元二次方程的两个实数根恰为另两个字母,根据判别式求出所需字母的范围。解:因为x+y=5-z,xy=3-z(y+x)=3-z(5-z)=z2-5z+3,所以x、y是关于t的一元二次方程t2-(5-z)t+z2-5z+3=0的两个实根,因为![]() ,即3z2-10z-13≤0,
,即3z2-10z-13≤0,![]() ,所以z≤
,所以z≤![]() ,当x=y=
,当x=y=![]() 时,z=
时,z=![]() ,故此时z的最大值为
,故此时z的最大值为![]()
构造含参数的一元二次方程,利用判别式求字母的取值范围套路不清晰。







