如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=6，AB=3．E为BC边上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧．

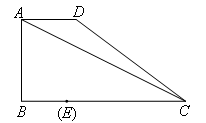
（1）当正方形的顶点F恰好落在对角线AC上时，线段BE的长为       ；将此正方形BEFG沿BC向右平移，记平移中的正方形BEFG为正方形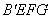，当点E与点C重合时停止平移．设平移的距离为t，则t的取值范围是      ．(    )

• A.2，
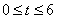
• B.2，
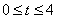
• C.，
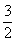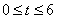
• D.，

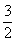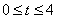
答案

正确答案：B

知识点：相似三角形的判定和性质  图形运动产生的面积问题  

如图，

设正方形BEFG的边长为x，
则BE=GF=BG=x．
∵AB=3，BC=6，
∴AG=AB-BG=3-x．
∵GF∥BE，
∴△AGF∽△ABC，
∴，即，
解得x=2，即BE=2．
上图为图形平移的初始时刻，此时CE=4，
从开始平移到点E与点C重合时，即停止平移时，平移的距离为4，
故t的取值范围是．

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>