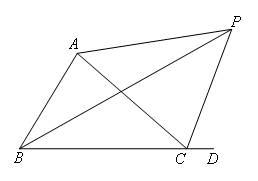
如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P．
若∠BPC=40°，则∠CAP等于(    )

1．思路点拨
①见到两条角平分线相交，考虑角平分线的性质，过点P分别向角的两边作垂线，垂线段相等．
②借助常见结构：找到∠BPC和∠BAC的关系，求出∠BAC的度数．
③借助三角形的内角和定理和平角解决问题．
2．解题过程
解：如图，

过点P分别向BC，AC，BA边所在直线作垂线，垂足分别为点E，F，G，
由题意得：∠1=∠2，∠3=∠4
∵
∴∠BAC=2∠BPC=80°
∴∠CAG=∠5+∠6=100°
在Rt△CEP和Rt△CFP中，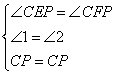

∴Rt△CEP≌Rt△CFP（AAS）
∴PE=PF
同理可证，PE=PG
∴PF=PG
在Rt△AFP和Rt△AGP中，

∴Rt△AFP≌Rt△AGP（HL）
∴∠5=∠6
∵∠5+∠6=100°
∴∠5=∠6=50°
即∠CAP=50°，选C
3．易错点
①对于数学中“见到什么想什么”，模块化的思维掌握不好，见到角平分线不知道作垂线找思路；
②不清楚常见的角平分线结构，三角形的两条内角平分线相交、一条内角平分线和一条外角平分线相交、两条外角平分线相交所成的角与已知三角形角度之间的关系．

略