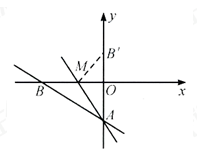
如图，直线分别与y轴、x轴交于点A和点B，M是OB上一点，若将△ABM沿AM折叠，点B恰好落在y轴上的点B'处，则直线AM的解析式为（）

• A.
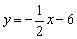
• B.
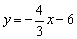
• C.
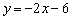
• D.

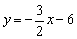
答案

正确答案：C

知识点：翻折变换（折叠问题）  

利用折叠的轴对称性可得BM=B^‘M，
设OM的长度为a，则B^‘M=8-a，
在Rt△B^‘MO中，由勾股定理可得a=3，
从而得到M的坐标
根据A、M两点的坐标得到AM的解析式.

不能熟练应用折叠的本质特征

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>