如图:有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形.依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的为()
- A.
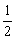
- B.
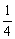
- C.
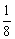
- D.
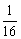
答案
正确答案:B
知识点:翻折变换(折叠问题)
由于折叠一次后得到的等腰直角三角形与原等腰直角三角形是相似三角形,得到的相似比=现在的斜边:原来的斜边=![]() ,
,
∴折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的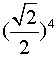 =
=![]() 倍.
倍.
(1)折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
(2)等腰直角三角形的性质,相似三角形的性质求解.学生对于这两部分考虑不周全。








