如图,在平面直角坐标系中,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,点D是线段AB上一动点(可与端点重合),过点B作BN⊥CD于点N(可与端点重合),当点D从点A运动到点B的过程中,点N运动的路径长为( )
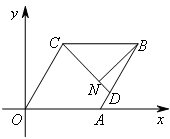
- A.
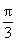
- B.
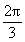
- C.
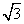
- D.2
答案
正确答案:B
点D在AB上运动时,点N也随之运动,要求点N运动的路径长,首先要确定点N运动的路径是什么样的,就需要分析与点N运动过程有关的定点、动点.
在点N运动的过程中,BN⊥CD不变,也即∠CNB为一个直角不变,同时菱形OABC的位置和大小都不发生变化,也就是△CNB是一个直角三角形,且斜边BC不发生变化,则点N运动轨迹在以BC为直径的圆上,如图所示(设圆心为点F).
在判断完点N的运动轨迹为圆弧之后,需要确定圆心角的度数,需要确定起点终点的位置.
当点D在点A时,此时点N位于起始位置,如图所示,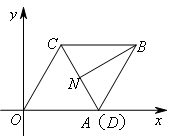
当点D位于点B时,点N与点B重合,
∴点N运动的轨迹如图所示,圆心角(∠BFN)的度数为120°,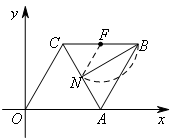
∴点N的运动路径长为![]() .
.
略








