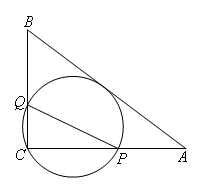
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
- A.4.75
- B.4.8
- C.
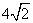
- D.9.6
答案
正确答案:B
由于点P、Q都是动点,没有办法直接进行研究,需要挖掘不变特征进行转化,考虑点C是直角顶点,∠BCA=90°是不变的,可以得到PQ是圆的直径,进而考虑求直径的最小值即可;
如图,设圆与AB相切于点D,连接CD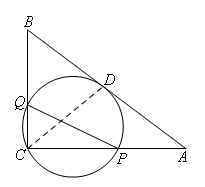
∵∠QCP为直角,
∴PQ为直径
∴![]()
∴当CD长度最小,且为直径时,PQ=CD,满足PQ长度最小
显然当CD⊥AB时,CD的长度最小,此时CD=4.8,
即PQ的最小值为4.8
PQ长度最小时,如图所示(以CD为直径作圆)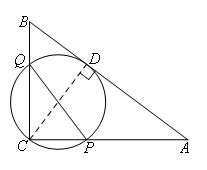
略








