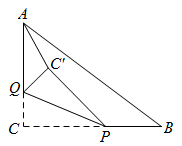
如图，在Rt△ACB中，∠ACB=90°，AC=6，BC=8，P，Q分别是边BC，AC上的动点．将△PCQ沿PQ翻折，C点的对应点为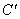
，连接
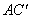，则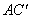的最小值是( )
- A.2
- B.3
- C.4
- D.6
答案
正确答案：A
知识点：几何最值问题 翻折变换（折叠问题）
由题意得AB=10．
由折叠可知，
，
，即
为定值8．
要求
的最小值，只需求出
的最小值即可．
根据两点之间线段最短可知，的最小值是AB的长．
∴的最小值为2．
此时点P与点B重合，折叠后点C的对应点
落在AB．
故选A．
略
WORD格式（
