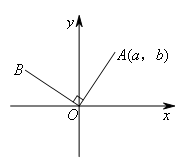
如图，已知点A（a，b），O是原点，OA=OB，OA⊥OB，则点B的坐标是(    )

如图，过点B作BF⊥x轴于点F，过点A作AE⊥x轴于点E.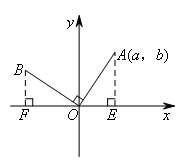

∵点A（a，b），
∴OE=a，AE=b.
∵OA⊥OB，
∴∠BOF+∠AOE=90°．
又∵∠BOF+∠OBF=90°，
∴∠AOE=∠OBF．
又∵∠OEA=∠BF0=90°，OA=OB，
∴△AOE≌△OBF（AAS），
∴OF=AE=b，BF=OE=a．
∵点B在第二象限，
∴点B的坐标是（-b，a）.
故选D.

略