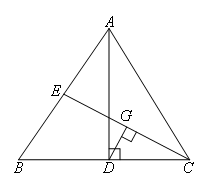
已知:如图,在△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE,G为垂足.则下列说法一定正确的是(    )
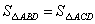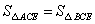①;②;③G是CE的中点;④∠B=2∠BCE.

结论①，②：三角形的中线平分三角形的面积，故①不正确，②正确．
结论③：如图，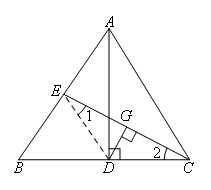

连接DE，
∵AD⊥BC，
∴∠ADB=90°，
又∵E为AB的中点，
∴，
∵DC=BE，
∴DC=DE，
又∵DG⊥CE，
∴G为CE的中点．故③正确.
结论④：
由③中可知，∠B=∠BDE，
∠BDE=∠1+∠2，
又∵∠1=∠2，
∴∠BDE=2∠2，
∴∠B=2∠2，
即∠BDE=2∠BCE．故④正确．
②③④正确，故选B．

略