如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是(    )

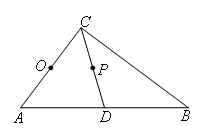
• A.点P在⊙O内
• B.点P在⊙O上
• C.点P在⊙O外
• D.无法确定

答案

正确答案：A

知识点：直角三角形斜边上的中线  点与圆的位置关系  

⊙O的半径r，只需要判断OP的长d与半径r的关系即可．当时，点P在圆外；
当时，点P在圆上；当时，点P在圆内．
如图，连接OP，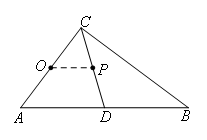

由题意得，OP是△CAD的中位线，
∴．
∵OC=3，
∴，
∴点P在⊙O内．

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>