如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,
点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;
④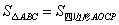 .其中所有正确结论的序号为( )
.其中所有正确结论的序号为( )
- A.①②③
- B.①②④
- C.①③④
- D.①②③④
答案
正确答案:D
知识点:等边三角形的判定与性质 截长补短法
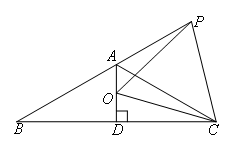
如图,连接OB,
∵AB=AC,AD⊥BC,∠BAC=120°,
∴BD=CD,∠BAD=∠CAD=60°,此时AD是BC的垂直平分线,
∴OB=OC,∠ABC=30°.
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°.
∴结论①正确.
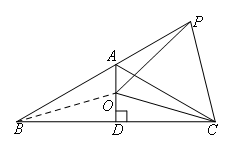
如图,延长线段BO得射线BE,
由题意可知,∠POE=∠OPB+∠OBP,∠COE=∠OBC+∠OCB,
∴∠POC=∠POE+∠COE=∠OPB+∠OBP+∠OBC+∠OCB=60°.
∵OP=OC,
∴△OPC是等边三角形,
∴结论②正确.
如图,在线段AC上截取AF=AP,
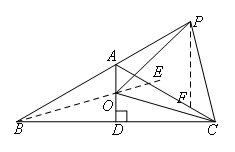
∵∠PAF=60°,
∴△AFP是等边三角形,
∴AP=PF,∠APF=60°.
∵△OPC是等边三角形,
∴∠OPC=60°,OP=PC,
∴∠APO=∠FPC,
∴△PAO≌△PFC,
∴AO=FC,
∴AC=AF+FC=AP+AO,
∴结论③正确.
如图,过点C作CG⊥PB于点G,
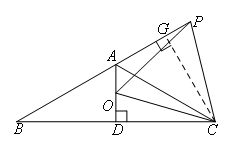
∵∠DAC=∠PAC=60°,CD⊥AD,
∴CG=CD,
∴![]() .
.
∵AC=AO+AP,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴结论④正确.
略








