如图,在等腰三角形ABC中,AB=AC,E是AC延长线上一点,F是AB上一点,连接EF交BC于点D,且满足D是EF中点,则( )
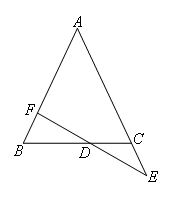
- A.AF=BC
- B.BD=CD
- C.CD=CE
- D.BF=CE
答案
正确答案:D
知识点:全等三角形的性质与判定 类倍长中线
如图,过点F作FG∥AC交BC于点G.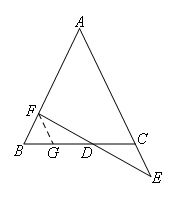
∴∠DFG=∠E,
∵D是EF的中点,
∴DF=DE,
∵∠FDG=∠EDC,
∴△FDG≌△EDC,
∴FG=CE,
∵FG∥AC,AB=AC,
∴∠FGB=∠ACB,∠B=∠ACB,
∴∠FGB=∠B,
∴FG=BF,
∴BF=CE.
故选D
略








