如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,
∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则点B′的坐标为( )
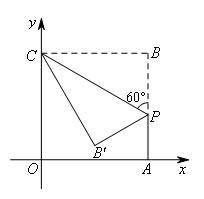
- A.

- B.
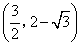
- C.
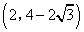
- D.
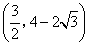
答案
正确答案:C
知识点:折叠问题 含30°角的直角三角形 求点的坐标
思路:根据坐标的定义,要求点的坐标,需要过这一点向x轴或y轴作垂线.
如图,过点B′作B′D⊥OC于点D.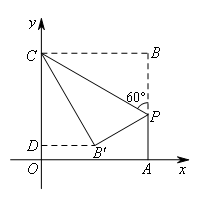
∵点A的坐标是(4,0),
∴OA=4,即正方形的边长为4.
在正方形OABC中,∠CPB=60°,
∴∠BCP=30°.
由折叠的性质知,CB′=CB=4,∠B′CP=∠BCP =30°,
∴∠B′CD=30°,
∴![]() ,
,
∴![]() .
.
∴点B′的坐标为![]() .
.
故选C.
略








