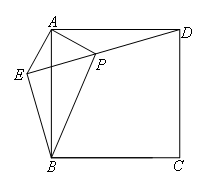
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.
若AE=AP=1,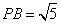.下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为;
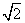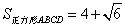④S_△APD+S_△APB=1+;⑤.其中正确结论的序号是(    )

①∠EAB+∠BAP=90°，∠PAD+∠BAP=90°，
∴∠EAB=∠PAD，
又∵AE=AP，AB=AD，
∴△APD≌△AEB．
故结论①正确．
②如图，

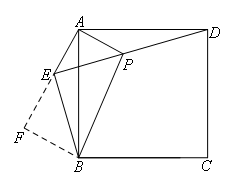
过B作BF⊥AE，交AE的延长线于F，
∵AE=AP，∠EAP=90°，
∴∠AEP=∠APE=45°，
∴∠AEB=∠APD=135°，
∴∠PEB=90°，
∴EB⊥ED，故结论②正确．
③∵∠PEB=90°，∠AEP=45°，
∴∠FEB=45°，
∴△EFB是等腰直角三角形，
在Rt△AEP中，，
在Rt△PEB中，，
∴，
∴Rt△EFB中，．
故结论③错误．
④△APD与△APB的面积之和即为四边形AEBP的面积，同时也是△AEP和△PEB的面积之和，S_△AEP+S_△PEB=×1×1+××=+，故结论④错误．
⑤在Rt△ABF中，，
∴，故结论⑤正确．
故正确的结论是①②⑤．

略