如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
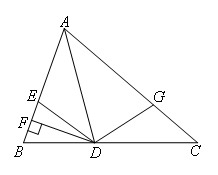
- A.11
- B.5.5
- C.7
- D.3.5
答案
正确答案:B
知识点:角平分线的性质 三角形的面积 全等三角形的判定和性质
1.思路点拨
①见到角平分线和一边上的高,考虑角平分线的性质,故需过点D向AC作垂线;
②根据线段相等,考虑放到两个三角形中证明三角形全等,利用全等三角形的性质:全等三角形的面积相等,可以转移面积;
③根据不同三角形之间的面积关系,结合已知求解目标.
2.解题过程
如图,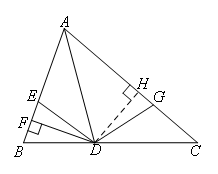
过点D作DH⊥AC,垂足为H
∵AD平分∠BAC
∴DH=DF
在Rt△DEF和Rt△DGH中![]() ,
,
∴Rt△DEF≌Rt△DGH(HL)
∴![]() ,
,
在Rt△ADF和Rt△ADH中![]() ,
,
∴Rt△ADF≌Rt△ADH(HL)
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() .
.
故选B
3.易错点
①见到什么想什么,模块化思维比较弱,不能从角平分线和一边上的高想到作另外一边的垂线;
②能想到作垂线,但是不能想到三角形全等,利用三角形全等转移面积.
略








