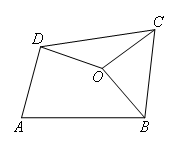
如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO的度数是(    )

如图，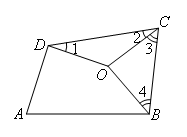

∵OB=OC=OD
∴∠1=∠2，∠3=∠4
∵∠BCD=75°
∴∠2+∠3=75°
∴∠1+∠4=75°
∵四边形ABCD的内角和为360°，∠BAD=75°
∴∠ADO+∠ABO=360°-(∠2+∠3)-(∠1+∠4)-∠A
=∠360°-75°-75°-75°=135°
故选B．

略