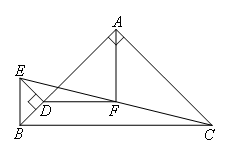
已知:如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,垂足分别为点A,点D,连接EC,F为EC中点,连接AF,DF,则AF,DF的数量关系和位置关系是(    )

1．思路点拨
F为EC的中点，我们同样可以采取倍长的方法，但是在倍长DF的时候，点不一定落在AC上，所以为了避免证明点在直线上，我们换一种作辅助线的方法，采取延长的方法，再证明全等，达到和倍长中线一样的效果，这种结构叫做平行线加中点结构．
2．解题过程
AF⊥DF，AF=DF，理由如下：
如图，延长DF交AC于点P.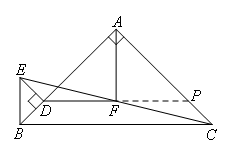

∵BA⊥AC，ED⊥BD
∴∠BAC=∠EDA=90°
∴DE∥AC
∴∠DEC=∠ECA
∵F为EC中点
∴EF=FC
在△EDF和△CPF中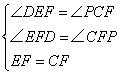

∴△EDF≌△CPF（AAS）
∴DE=CP，DF=PF
∵△ABC与△BDE均为等腰直角三角形
∴AB=AC，DE=BD
∴AB-BD=AB-DE=AC-CP
即AD=AP
在△DAF和△PAF中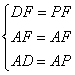

∴△DAF≌△PAF（SSS）
∴∠DFA=∠PFA=90°，∠DAF=∠PAF=45°
∴AF⊥DF，AF=DF
故选D

略