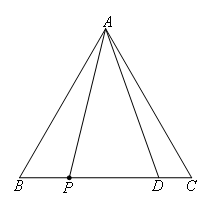
已知:如图,在等边△ABC中,AB=10,D为边BC上一点,且BD=8.动点P从点B出发沿BC-CA方向以每秒2个单位的速度向点A运动,连接AD,AP,BP.设点P运动的时间为t秒.若△ABP和△ADC全等,则t的值为(    )

分析P点的运动状态可知：0≤t≤10，且点P在点C处发生了状态改变，所以可分成两种情况，即点P在BC上，点P在CA上运动．
①当点P在BC上运动时，△ABP和△ADC全等，由于未用全等符号连接，可知应该分类讨论．
分析：在△ABP和△ADC中，∠B=∠C，AB=AC，点A和点A是对应顶点，
∴B和C一定是对应顶点，也就是说仅有一种情况，即△ABP≌△ACD．
如图，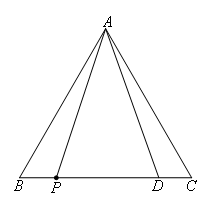

由△ABP≌△ACD
可得，BP=CD，
在等边△ABC中，AB=BC=CA
又∵AB=10，
∴BC=10
∵BD=8，
∴BP=CD=2
BP=2t
∴t=1
②当点P在CA上运动时，△ABP和△ADC全等，由于未用全等符号连接，可知应该分类讨论．
分析：在△ABP和△ADC中，∠BAC=∠C，AB=AC，点A和点C是对应顶点，
∴B和A一定是对应顶点，也就是说仅有一种情况，即△ABP≌△CAD．
如图，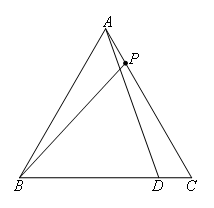

∵△ABP≌△CAD
∴AP=CD=2
∴CP=8
又∵BC+CP=2t=18
∴t=9
故选C

略