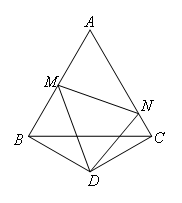
如图,△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB,AC于M,N两点,连接MN,形成一个三角形,则△AMN的周长为(    )

1．思路点拨
①首先看求解目标：△AMN的周长，即AM+MN+AN，三条线段都在变化，必须把变量和固定不变的线段建立联系；
②结合题目等边三角形和等腰三角形都有线段相等，而有线段相等可以考虑证明它们所在的三角形全等，借助全等集中线段．
2．解题过程
如图，

在AC延长线上截取CE=BM，
∵△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，
∴∠ABC=∠ACB=60°，∠DBC=∠DCB=30°，
∴∠ABD=∠ACD=90°，
∴∠DCE=90°，
∵BD=CD，
∵在△BDM和△CDE中，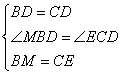

∴△BDM≌△CDE（SAS）
得MD=ED，∠1=∠2，
∵∠1+∠3+∠MDN=120°，∠MDN=60°
∴∠1+∠3=60°
∴∠2+∠3=60°，即∠EDN=60°
在△MDN和△EDN中，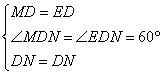

∴△MDN≌△EDN（SAS），
∴MN=EN
∵EN=CE+CN=BM+CN
故△AMN的周长=AM+MN+AN=AM+AN+EN=AM+BM+AN+CN=AB+AC=2．
故选A
3．易错点
①遇到三条线段都在变化的题，缺乏基本的处理思路，不知道把变量和不变量联系起来；
②具体操作方法不会，见到线段相等比较多，不知道寻找全等三角形来转移线段．

略