如图，E、F分别是三角形ABC中BC边与AC边上的点，AE与BF交于点O，且三角形AFO、三角形ABO和三角形BEO的面积依次为3、2、1。求四边形EOFC的面积是（）。

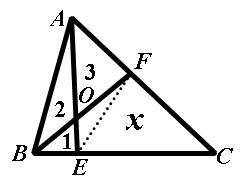如图，连接EF，三角形ABO的面积是三角形BEO的两倍，而它们的高相等，所以AO：OE=2:1。故三角形AOF的面积：三角形EOF的面积=2:1。所以三角形EOF的面积就是：3÷2=1.5。然后可以根据两个三角形的高相等，面积比就是对应底的比，所以。设三角形EFC的面积是x,则，，交叉相乘，可以得到，解得。所以四边形EOFC的面积是：1.5+22.5=24。答案为D。

面积比与线段之间的关系